The Cartesian Plane

The Cartesian plane consists of two directed lines that perpendicularly intersect their respective zero points.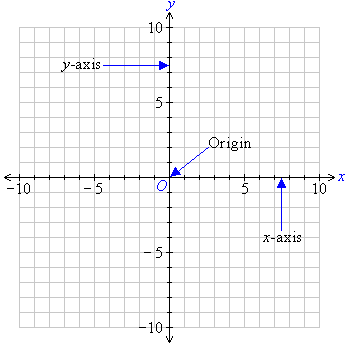 The horizontal directed line is called the x-axis and the vertical directed line is called the y-axis.  The point of intersection of thex-axis and the y-axis is called the origin and is denoted by the letter O. The Coordinates The position of any point on the Cartesian plane is described by using two numbers:  (x, y).  The first number, x, is the horizontal position of the point from the origin.  It is called the x-coordinate. The second number, y, is the vertical position of the point from the origin.  It is called the y-coordinate.  Since a specific order is used to represent the coordinates, they are called ordered pairs. 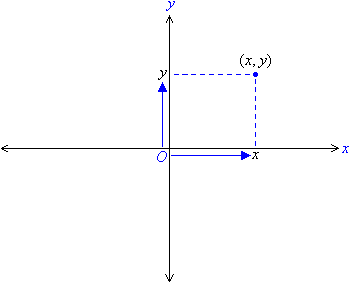For example, the ordered pair (5, 8) represents a point 5 units to the right of the origin in the direction of the x-axis and 8 units above the origin in the direction of the y-axis as shown in the diagram below. We say that: The x-coordinate of point P is 5; and the y-coordinate of point P is 8. Or simply, we can say that: The coordinates of point P are (5, 8). Note the following: For the point P(5, 8), the ordered pair is (5, 8).  So: 5 is the x-coordinate, and 8 is the y-coordinate. P(5, 8) means P is 5 units to the right of and 8 units above the origin. 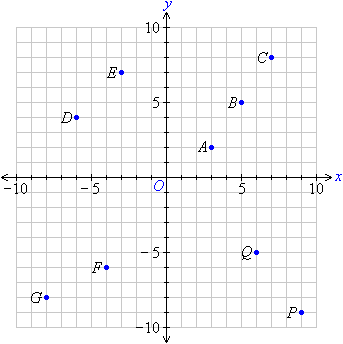Example 1 State the coordinates of each of the points shown on the Cartesian plane: Solution: A is 3 units to the right of and 2 units above the origin.  So, point A is (3, 2). B is 5 units to the right of and 5 units above the origin.  So, point B is (5, 5). C is 7 units to the right of and 8 units above the origin.  So, point C is (7, 8). D is 6 units to the left of and 4 units above the origin.  So, point D is (–6, 4). E is 3 units to the left of and 7 units above the origin.  So, point E is (–3, 7). F is 4 units to the left of and 6 units below the origin.  So, point F is (–4, –6). G is 8 units to the left of and 8 units below the origin.  So, point G is (–8, –8). P is 9 units to the right of and 9 units below the origin.  So, point P is (9, –9). Q is 6 units to the right of and 5 units below the origin.  So, point Q is (6, –5). Distance Formula The Distance formula can be obtained by creating a triangle and using the Pythagorean Theorem to find the length of the hypotenuse. The hypotenuse of the triangle will be the distance between the two points. The subscripts refer to the first and second points; it doesn't matter which points you call first or second. x2 and y2 are the x,y coordinates for one point x1and y1 are the x,y coordinates for the second point d is the distance between the two points Midpoint Formula Midpoint Formula is the formula for the midpoint between points (x1, y1) and (x2, y2). Note that this is simply the average of the x-coordinates and the average of the y-coordinates. Slope Formula Sometimes called 'Rise over Run' The formula for the slope of the straight line going through the points (x1, y1) and (x 2, y 2) is given by: The subscripts refer to the two points. (m=rise/run)  Note: Parallel lines have equal slope. Perpendicular lines have negative reciprocal slopes. (c) http://www.mathsteacher.com.au/