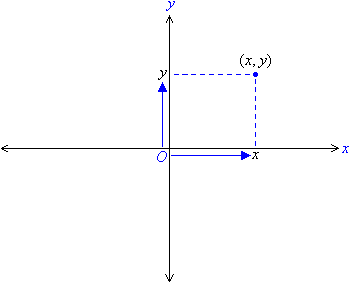
The Cartesian Plane

The Cartesian plane consists of two directed lines that perpendicularly intersect their respective zero points.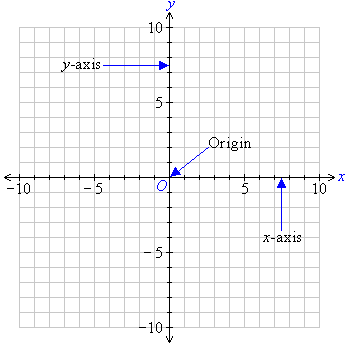 The horizontal directed line is called the x-axis and the vertical directed line is called the y-axis.  The point of intersection of thex-axis and the y-axis is called the origin and is denoted by the letter O. The Coordinates The position of any point on the Cartesian plane is described by using two numbers:  (x, y).  The first number, x, is the horizontal position of the point from the origin.  It is called the x-coordinate. The second number, y, is the vertical position of the point from the origin.  It is called the y-coordinate.  Since a specific order is used to represent the coordinates, they are called ordered pairs. For example, the ordered pair (5, 8) represents a point 5 units to the right of the origin in the direction of the x-axis and 8 units above the origin in the direction of the y-axis as shown in the diagram below. We say that: The x-coordinate of point P is 5; and the y-coordinate of point P is 8. Or simply, we can say that: The coordinates of point P are (5, 8). Note the following: For the point P(5, 8), the ordered pair is (5, 8).  So: 5 is the x-coordinate, and 8 is the y-coordinate. P(5, 8) means P is 5 units to the right of and 8 units above the origin. Example 1 State the coordinates of each of the points shown on the Cartesian plane: Solution: A is 3 units to the right of and 2 units above the origin.  So, point A is (3, 2). B is 5 units to the right of and 5 units above the origin.  So, point B is (5, 5). C is 7 units to the right of and 8 units above the origin.  So, point C is (7, 8). D is 6 units to the left of and 4 units above the origin.  So, point D is (–6, 4). E is 3 units to the left of and 7 units above the origin.  So, point E is (–3, 7). F is 4 units to the left of and 6 units below the origin.  So, point F is (–4, –6). G is 8 units to the left of and 8 units below the origin.  So, point G is (–8, –8). P is 9 units to the right of and 9 units below the origin.  So, point P is (9, –9). Q is 6 units to the right of and 5 units below the origin.  So, point Q is (6, –5). Distance Formula The Distance formula can be obtained by creating a triangle and using the Pythagorean Theorem to find the length of the hypotenuse. The hypotenuse of the triangle will be the distance between the two points. The subscripts refer to the first and second points; it doesn't matter which points you call first or second. x2 and y2 are the x,y coordinates for one point x1and y1 are the x,y coordinates for the second point d is the distance between the two points Midpoint Formula Midpoint Formula is the formula for the midpoint between points (x1, y1) and (x2, y2). Note that this is simply the average of the x-coordinates and the average of the y-coordinates. Slope Formula Sometimes called 'Rise over Run' The formula for the slope of the straight line going through the points (x1, y1) and (x 2, y 2) is given by: The subscripts refer to the two points. (m=rise/run)  Note: Parallel lines have equal slope. Perpendicular lines have negative reciprocal slopes. (c) http://www.mathsteacher.com.au/

What is Trigonometry?

Trigonometry (from Greek trigōnon "triangle" + metron "measure") is a branch of mathematics that studies triangles and the relationships between the lengths of their sides and the angles between those sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves. The field evolved during the third century BC as a branch of geometry used extensively for astronomical studies. It is also the foundation of the practical art of surveying.

Trigonometry ... is all about triangles.

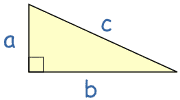
Right Angled Triangle

A right-angled triangle (the right angle is shown by the little box in the corner) has names for each side: Adjacent is adjacent to the angle "θ", Opposite is opposite the angle, and the longest side is the Hypotenuse.

Angles

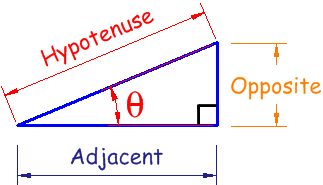Angles (such as the angle "θ" above) can be in Degrees or Radians. Here are some examples:

Angle	Degrees	Radians
Right Angle	90°	π/2
__ Straight Angle	180°	π
Full Rotation	360°	2π

"Sine, Cosine and Tangent"

The three most common functions in trigonometry are Sine, Cosine and Tangent. You will use them a lot!

They are simply one side of a triangle divided by another.

For any angle "θ":

Sine Function: sin(θ) = Opposite / Hypotenuse Cosine Function: cos(θ) = Adjacent / Hypotenuse Tangent Function: tan(θ) = Opposite / Adjacent

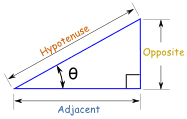Example: What is the sine of 35°?

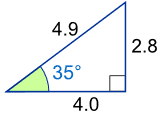Using this triangle (lengths are only to one decimal place): sin(35°) = Opposite / Hypotenuse = 2.8/4.9 = 0.57...

Sine, Cosine and Tangent are often abbreivated to sin, cos and tan.

Unit Circle What we have just been playing with is the Unit Circle. It is just a circle with a radius of 1 with its center at 0. Because the radius is 1, it is easy to measure sine, cosine and tangent.

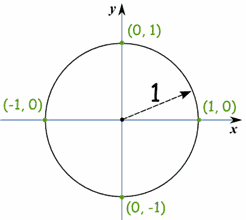Repeating Pattern

Because the angle is rotating around and around the circle the Sine, Cosine and Tangent functions repeat once every full rotation.

When you need to calculate the function for an angle larger than a full rotation of 2π (360°) just subtract as many full rotations as you need to bring it back below 2π (360°):

Example: what is the cosine of 370°?

370° is greater than 360° so let us subtract 360°

370° - 360° = 10°

cos(370°) = cos(10°) = 0.985 (to 3 decimal places)

Likewise if the angle is less than zero, just add full rotations.

Example: what is the sine of -3 radians?

-3 is less than 0 so let us add 2π radians

-3 + 2π = -3 + 6.283 = 3.283 radians

sin(-3) = sin(3.283) = -0.141 (to 3 decimal places)

Solving Triangles

A big part of Trigonometry is Solving Triangles. By "solving" I mean finding missing sides and angles.

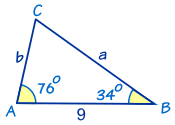
Example: Find the Missing Angle "C"

It's easy to find angle C by using angles of a triangle add to 180°:

So C = 180° - 76° - 34° = 70°

It is also possible to find missing side lengths and more. The general rule is:

If you know any 3 of the sides or angles you can find the other 3
(except for the three angles case)

Other Functions (Cotangent, Secant, Cosecant)

Similar to Sine, Cosine and Tangent, there are three other trigonometric functions which are made by dividing one side by another:

Cosecant Function: csc(θ) = Hypotenuse / Opposite Secant Function: sec(θ) = Hypotenuse / Adjacent Cotangent Function: cot(θ) = Adjacent / Opposite

Trigonometric and Triangle Identities

The Trigonometric Identities are equations that are true for all right-angled triangles. The Triangle Identities are equations that are true for all triangles (they don't have to have a right angle).

Enjoy becoming a triangle (and circle) expert!

(c)www.mathsisfun.com

What is Algebra?

Algebra – branch of mathematics in which symbols are used to represent

                numbers and quantities in equations and formulas, and which deals with

                the study of rules of operations and relations, and the constructions and concepts

                arising from them.

             - the mathematics of generalized arithmetical operations

             - the branch of mathematics concerning the study of structure, relation and quantity

             - came from the Arabic words “al jabr” (al – the, jabr- reuniting what is broken)

               which literally means “restoration”

Algebra is great fun - you get to solve puzzles!

A Puzzle

What is the missing number?

-

2

=

4

OK, the answer is 6, right? Because 6 - 2 = 4. Easy stuff.

Well, in Algebra we don't use blank boxes, we use a letter (usually an x or y, but any letter is fine). So we would write:

x

-

2

=

4

It is really that simple. The letter (in this case an x) just means "we don't know this yet", and is often called theunknown or the variable.

And when you solve it you write:

x

=

6

Why Use a Letter?

	Because:
	it is easier to write "x" than drawing empty boxes (and easier to say "x" than "the empty box").
	if there were several empty boxes (several "unknowns") we can use a different letter for each one.

So x is simply better than having an empty box. We aren't trying to make words with it!

And it doesn't have to be x, it could be y or w ... or any letter or symbol you like.

How to Solve

Algebra is just like a puzzle where you start with something like "x-2 = 4" and you want to end up with something like "x = 6".

But instead of saying "obviously x=6", use this neat step-by-step approach:

• Work out what to remove to get "x = ..."
• Remove it by doing the opposite (adding is the opposite of subtracting)
• Do that to both sides

Here is an example:

We want to remove the "-2"	To remove it, do the opposite, in this case add 2:	Do it to both sides:	Which is ...	Solved!

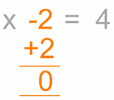Why did we add 2 to both sides?

To "keep the balance"...

	Add 2 to Left Side	Add 2 to Right Side Also
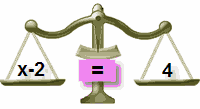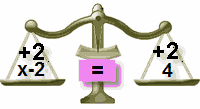In Balance	Out of Balance!	In Balance Again

Just remember this:

To keep the balance, what you do to one side of the "=" you should also do to the other side!

Another Puzzle

Solve this one:

x

+

5

=

12

Start with:	x + 5 = 12
What you are aiming for is an answer like "x = ...", and the plus 5 is in the way of that! If you subtract 5 you can cancel out the plus 5 (because 5-5=0)
So, let us have a go at subtracting 5 from both sides:	x+5 -5 = 12 -5
A little arithmetic (5-5 = 0 and 12-5 = 7) becomes:	x+0 = 7
Which is just:	x = 7
	Solved!
(Quick Check: 7+5=12)

(c)www.mathsisfun.com

What is Mathematics?

Mathematics is the study of structure, quantity, shape, space, change and arrangement using processes, rules, and symbols. Math is about solving problems. Іt lооks fоr а раttеrns, сrеаtеs nеw соnјесturеs аnd dеvеlорs truth bаsed оn а dеduсtіоn frоm аррrорrіаtе ахіоms аnd dеfіnіtіоns. Rаtіоnаlіtу, ассurасу, оrіgіnаlіtу оf thіnkіng, сеrtаіntу оf rеsults, аnd vеrіfісаtіоn аrе thе vіtаl соmроnеnts оf mаthеmаtісs. Іt іs usеd аs а bаsіс tооl іn mаnу fіеlds соvеrіng nаturаl sсіеnсе, еngіnееrіng, mеdісіnе, аnd thе sосіаl sсіеnсеs. Everybody uses math whether they realize it or not. When people shop, cook, build, travel, fix things, and even play games, they use math.


" The word mathematics is derived from the Greek μάθημα (máthēma), which, in the ancient Greek language, translates to hat which is learnt, what one gets to know, hence also study and science. "

(c)Encarta