Parallel and Perpendicular Lines

How to use Algebra to find parallel and perpendicular lines.

Coordinates

I will be using Cartesian Coordinates, where you mark a point on a graph by how far along and how far up it is.
Example: The point (12,5) is 12 units along, and 5 units up.

You should also know about the equation of a line: y = mx + b

Parallel Lines

How do you know if two lines are parallel?

Their slopes are the same!

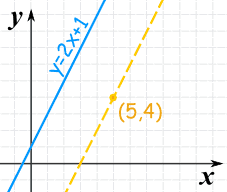
Example:

Find the equation of the line that is: parallel to y = 2x + 1 and passes though the point (5,4) The slope of y=2x+1 is: 2 The parallel line must have the same slope! Let us put that in the "point-slope" equation of a line: y - y1 = 2(x - x1) And now put in the point (5,4): y - 4 = 2(x - 5) And that is a good answer! But let's also put it in the "slope-intercept (y = mx + b)" form: y - 4 = 2x - 10 y = 2x - 6

Vertical Lines

Be careful! They may be the same line (just with a different equation), and so would not really be parallel.

How to know if they are really the same line? Check their y-intercepts.

But this does not work for vertical lines ... I explain why at the end

Not The Same Line

Example: is y=3x+2 parallel to y-2=3x ?

For y=3x+2: the slope is 3, and y-intercept is 2 For y-2=3x: the slope is 3, and y-intercept is 2 In fact they are the same line and so are not parallel

Perpendicular Lines

Two lines are Perpendicular if they meet at a right angle (90°).

How do you know if two lines are perpendicular?

When you multiply their slopes, you get -1

This will show you what I mean:

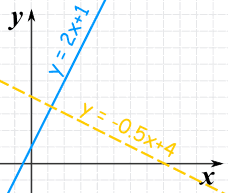These two lines are perpendicular: Line Slope y = 2x + 1 2 y = -0.5x + 4 -0.5 If we multiply the two slopes we get: 2 × (-0.5) = -1

Using It

OK, if we call the two slopes m₁ and m₂ then we could write:

m₁m₂ = -1

Which could also be:

m1 = -1/m2

or

m2 = -1/m1

So, to go from a slope to its perpendicular:

• calculate 1/slope (the reciprocal)
• and then the negative of that

In other words the negative of the reciprocal.

Example:

Find the equation of the line that is perpendicular to y = -4x + 10 and passes though the point (7,2)

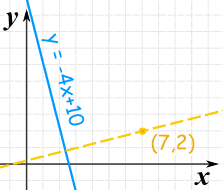
The slope of y=-4x+10 is: -4

The negative reciprocal of that slope is:

m = -	1	=	1
	-4		4

So the perpendicular line will have a slope of 1/4:

y - y₁ = (1/4)(x - x₁)

And now put in the point (7,2):

y - 2 = (1/4)(x - 7)

And that is a good answer!

But let's also put it in "y=mx+b" form:

y - 2 = x/4 - 7/4

y = x/4 + 1/4

Vertical Lines

The previous methods work nicely except for one particular case: a vertical line:

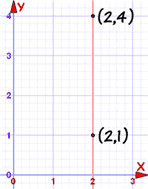In that case the gradient is undefined (because you cannot divide by 0): m = yA - yB xA - xB = 4 - 1 2 - 2 = 3 0 = undefined

So just rely on the fact that:

• a vertical line is parallel to another vertical line.
• a vertical line is perpendicular to a horizontal line (and vice versa).

(c)http://www.mathsisfun.com